Nie, nie, oczywiście nie będę namawiał żadnego z Was do uzyskiwania efektu guza na własnej głowie. Czasy biegania po pokoju i obijania się o wszelkie narożniki i ściany minęły. Ale ponieważ w duszy każdego z nas jest odrobinę dziecka, to będziemy nabijać inne guzy. Będzie to też nawiązanie do pierwszych, bardziej zaawansowanych gier 3D, w który efekt ten mogliśmy zaobserwować. Wywoływał wtedy rumieńce na buzi, ale bez guzów!
Skąd się więc biorą guzy?
Są dwie metody uzyskiwania bumpmuppingu. Jedna z nich, bardziej zaawansowana, polega na tym, że musimy posiadać dwie bitmapy aby uzyskać efekt. Jedna to oczywiście bitmapa, którą będziemy poddawać efektowi, druga stanowi tzw. mapę zniekształceń. Jest to bitmapa w odcieniach szarości gdzie jasność piksela odpowiada za wysokość oczekiwanego zniekształcenia - biały kolor najwyższy punkt, czarny najniższy. Mapa zniekształceń może, ale nie musi być niezależna od bitmapy źródłowej. Bitmapę źródłową może stanowić zapisana kartka papieru, a mapę zniekształceń będą stanowić biało czarne plamy. Obliczając wektor normalny do punktu na mapie zniekształceń (wektoro normalny, to wektor prostopadły do danego punktu) możemy się dowiedzieć jak "pochyły" jest punkt w stosunku do płaskiej powierzchni. Mając wektor normalny i wektor światła możemy określić jak światło opływa dany punkt (czy świeci z góry - jasno, czy z boku - ciemniej). W tym przypadku możemy uzyskac tekstury prezentującej pogniecioną kartkę. Metodę tą można uprościć, tj. kroki liczenia wektora normalnego i światła oraz ich interakcji. Ale o tym przy okazji drugiej metody.
Ta druga metoda nie korzysta z mapy zniekształceń. Tą obliczamy z samego obrazu źródłowego. Wadą jest oczywiście to, że np. mając wspomnianą kartę papieru nie poddamy jej efektowi pogniecenia, bo z niej samej nie uzyskamy takiej mapy zniekształceń. Mamy tu zazwyczaj dużo białej powierzchni i trochę ciemnych pikseli. Zniekształcenia będą występować tu głównie na granicach tych obszarów. Tak więc efekt jaki możemy uzyskać, to raczej coś w rodzaju wygrawerowanego czy wytłoczonego pisma - jasny kolor górka, ciemny kolor (pismo) dołek. Zbocza będą stanowić granice kolorów ciemnego i jasnego. Wszystko tu zależy od bitmapy wejściowej. Jeśli będzie prezentować owoc pomarańcza, to i końcowy efekt może być zadowalający. W przypadku obrazu kolorowego zamieniamy go po prostu na czarno-biały, ale tylko na potrzebę obliczenia mapy zniekształceń. Efekt końcowy oczywiście możemy zastosować do wejściowego obrazu kolorowego.
No dobra, ale skoro wspomniałem, że nie trzeba liczyć wektora normalnego oraz światła, to najwyższy czas oświecić nas jak to zrobić. Możemy tu zastosować uproszczenie, o którym zresztą już wspomniałem - może trochę w zaciemniony sposób, ale jednak. Mianowicie stosując założenie, że ciemny punkt jest najniżej, a jasny najwyżej, możemy obliczyć nachylenie powierzchni w danym punkcie jako różnicę jasności między nim, a sąsiadem. Jeśli obydwa będą ciemne, albo obydwa jasne, to mamy płaską powierzchnię, jeśli badany jest jasny, a kolejny ciemny, to znaczy, że mamy spadek, jeśli odwrotnie - górkę. W ten sposób obliczamy mapę zniekształceń.
A co ze światłem? Do światła zastosujemy gotową bitmapę. W środku jasne punkt, a zbliżając się do krawędzi ciemne - radialny gradient.
Jak to teraz połączyć. Na początek załóżmy, że bitmapa oraz tekstura ze światłem są identycznych wymiarów i światło świeci centralnie na środek bitmapy. Tak więc punkty 0,0 obydwu bitmap pokrywają się. Zaczynamy od punktu 1,1 i pobieramy z mapy zniekształceń różnicę jasności pomiędzy pikselami (1,1) oraz (0,1), czyli w osi poziomej (deltaX) oraz różnicę między pikselami (1,1) oraz (1,0) czyli w osi pionowej (deltaY). Mając obliczone te dwie wartości tworzymy z nich pseudowektor, który wyznacza w jakiej odległości od aktualnie przetwarzanego punktu mamy pobrać wartość światła (z tej radialnej tekstury). Po prostu dodajemy do aktualnego x,y obliczone wartości delta i mamy współrzędnego piksela z mapy światła. Jeśli aktualnie znajdowaliśmy się w punkcie (0,0) mapy światła, czyli ciemnym, ale delta była duża w obydwu kierunkach, to znaczy, że przeskoczyliśmy z ciemnego do jasnego punktu bitmapy światła. Co by się zgadzało, bo była to ostra "krawędź" do góry. Jeśli delty wynosiły 0, to pozostaniemy w tym samym punkcie światła, i to również się zgadza, bo oznacza to, że mamy do czynienia z płaską powierzchnią. W zależności od tego jakie są wartości deltaX oraz deltaY, skaczemy po naszej mapie światła w różnych kierunkach. Jeśli tekstura będzie mieć wszystkie piksele o jednakowym kolorze, to delty w każdym punkcie będą mieć wartości 0 i wynikiem będzie po prostu tekstura identyczna z teksturą światła. Natomiast czym bardziej różnorodne są piksele, tym "pomarszczenie" tekstury światła będzie większe. Jednak usuwając założenie, że światło świeci centralnie, ta sama krawędź może być doliną jeśli światło świeci z lewej strony, ale i górką jeśli światło świeci z prawej strony. Czyli to nasze "marszczenie" będzie pobierać punkt z mapy światła w zależności z jakiego punktu wystartujemy (gdzie będzie centralny punkt światła).
Na poniższym rysunku starałem się zwizualizować tą kwestię. Punkt numer 1 jest aktualnym punktem na mapie światła (albo początkowym, albo wynikającym z poprzedniego obliczenia). Delta między punktami 1 i 2 jest mniejsza niż między punktami 2 oraz 3, bo różnice jasności są inne. Szare krędzi to oczywiście bitmapa światła.
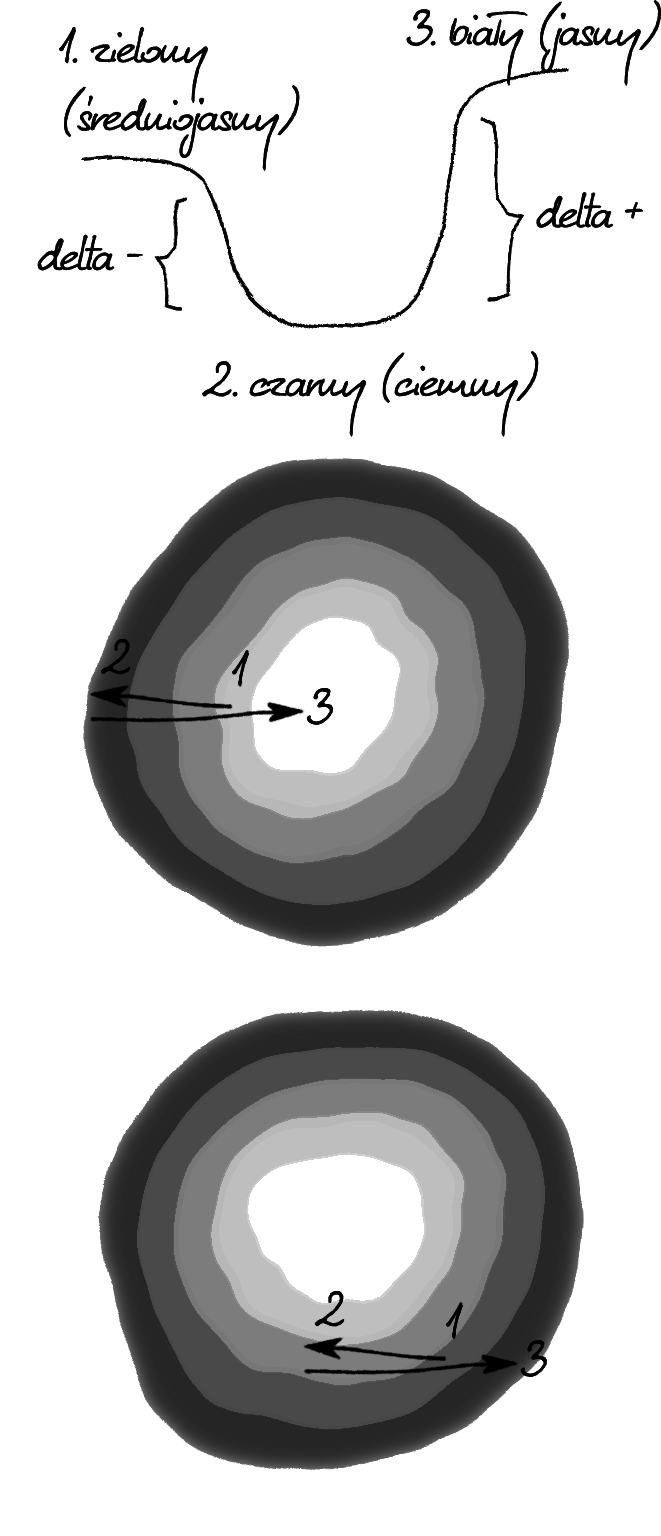
Jeśli nasza tekstura światła będzie tylko w odcieniach szarości i wynikowy efekt również chcemy uzyskać w takiej tonacji, to uzyskany z mapy światła piksel wstawiamy jako piksel wynikowy. Jeśli natomiast chcemy uzyskać efekt kolorowy, czyli nie tracić barw źródłowej tekstury, wtedy piksel tejże tekstury mnożymy przez wartość piksela światła, czyli po prostu albo go podjaśniamy, albo ściemniamy.
Oświeć mnie kodem!
Tyle na temat teorii. Warto będzie się przyjrzeć jak wygląda skrypt odpowiadający za ten efekt. No i oczywiście efekt... efektu! W tym wpisie będzie to bumpmapping czarno-biały.
<canvas id="canvas"></canvas>
+
/* nasz element <canvas>,
do którego wczytamy
obraz źródłowy
i wygenerujemy
docelowy
*/
const canvas = document.getElementById("canvas");
/* promień tekstury
światła
*/
const r = 300;
/* mapa światła
*/
const lightMap = [];
/* mapa zniekształceń
*/
const bumpMap = [];
/* generujemy mapę światła,
czyli ten radialny gradient
*/
for (let y = 0; y < r * 2; y++) {
for (let x = 0; x < r * 2; x++) {
/* natężenie światła liczymy jako
odległość danego punktu
od środka
*/
const intensity =
(1 -
Math.sqrt((x - r) * (x - r) + (r - y) * (r - y)) /
r) *
255;
if (lightMap[x] === undefined) lightMap[x] = [];
lightMap[x][y] = parseInt(intensity);
}
}
/* wczytujemy nasz
źródłowy obrazek
*/
let sourceImage = new Image();
sourceImage.onload = function() {
const width = this.width;
const height = this.height;
/* ustawiamy <canvas>
na wymiary takie
jak źródłowy obrazek
(i wynikowy)
*/
canvas.setAttribute("width", width);
canvas.setAttribute("height", height);
const ctx = canvas.getContext("2d");
/* kreślimy obrazek
na <canvas>
*/
ctx.drawImage(sourceImage, 0, 0);
/* i teraz możemy
pobrać wartości RGBA
każdego piksela
*/
const imagePixels = ctx.getImageData(0, 0, width, height);
/* tu będziemy liczyć nasze
deltaX oraz deltaY,
czyli mapę zniekształceń
*/
for (let y = 1; y < height; y++) {
for (let x = 1; x < width; x++) {
/* potrzebnę będą
wartości RGB piksela
aktualnego, na lewo,
oraz jeden wyżej
*/
const rXY =
imagePixels.data[y * (imagePixels.width * 4) + x * 4 + 0];
const gXY =
imagePixels.data[y * (imagePixels.width * 4) + x * 4 + 1];
const bXY =
imagePixels.data[y * (imagePixels.width * 4) + x * 4 + 2];
const rX1Y =
imagePixels.data[y * (imagePixels.width * 4) + (x - 1) * 4 + 0];
const gX1Y =
imagePixels.data[y * (imagePixels.width * 4) + (x - 1) * 4 + 1];
const bX1Y =
imagePixels.data[y * (imagePixels.width * 4) + (x - 1) * 4 + 2];
const rXY1 =
imagePixels.data[(y - 1) * (imagePixels.width * 4) + x * 4 + 0];
const gXY1 =
imagePixels.data[(y - 1) * (imagePixels.width * 4) + x * 4 + 1];
const bXY1 =
imagePixels.data[(y - 1) * (imagePixels.width * 4) + x * 4 + 2];
/* mając wartości RGB
w uproszczony sposób
obliczamy piksel
czarno-biały
*/
const grayXY = parseInt((rXY + gXY + bXY) / 3);
const grayX1Y = parseInt((rX1Y + gX1Y + bX1Y) / 3);
const grayXY1 = parseInt((rXY1 + gXY1 + bXY1) / 3);
/* teraz możemy
policzyć delty
*/
const deltaX = grayXY - grayX1Y;
const deltaY = grayXY - grayXY1;
if (bumpMap[x] === undefined) bumpMap[x] = [];
if (bumpMap[x][y] === undefined) bumpMap[x][y] = [];
/* wstawiamy je
do tablicy
zniekształceń
*/
bumpMap[x][y][0] = deltaX;
bumpMap[x][y][1] = deltaY;
}
}
/* przygotowujemy tablicę
dla wynikowych pikseli,
którą wstawimy do używanego
wcześniej <canvas>, bo obraz
źródłowy nie będzie nam potrzebny
*/
const newPixels = ctx.createImageData(width, height);
const newPixelsDataWidth = newPixels.width << 2;
/* możemy poruszać
myszą po ekranie,
czyli tak naprawdę
zmieniamy położenie
bitmapy światła
względem bitmapy obrazka,
to o czym pisałem wyżej,
w zależności, po której
stronie krawędzi jest
światło, ta albo jest
górką, albo doliną
*/
document.addEventListener("mousemove", function(e) {
/* tu łączymy mapę
zniekształceń
z mapą światła
*/
for (let y = 1; y < height; y++) {
for (let x = 1; x < width; x++) {
const offset = y * newPixelsDataWidth + (x << 2);
/* pobieramy delty
*/
const deltaX = bumpMap[x][y][0];
const deltaY = bumpMap[x][y][1];
/* czy badany punkt,
tj. xy+delta+kursor,
mieści się w mapie światła?
*/
if (
lightMap[x + deltaX + (r - e.clientX)] === undefined ||
lightMap[x + deltaX + (r - e.clientX)][
y + deltaY + (r - e.clientY)
] === undefined
) {
/* nie mieści się,
więc zakładamy,
że jest poza
mapą - ciemny
*/
newPixels.data[offset] = 0;
newPixels.data[offset + 1] = 0;
newPixels.data[offset + 2] = 0;
} else {
/* mieści się, więc
pobieramy go
*/
const intensity =
lightMap[x + deltaX + (r - e.clientX)][
y + deltaY + (r - e.clientY)
];
/* jasność punktu
światła stanowi
nowy piksel
na wynikowej
bitmapie
*/
newPixels.data[offset + 0] = intensity;
newPixels.data[offset + 1] = intensity;
newPixels.data[offset + 2] = intensity;
}
/* piksel nieprzezroczysty
*/
newPixels.data[offset + 3] = 255;
}
}
/* wstawiamy nowe piksele
do <canvas>
*/
ctx.putImageData(newPixels, 0, 0);
});
};
sourceImage.src = "dollar-517113_640.jpg";
Zobacz jaki efekt końcowy bumpmappingu 2D można osiągnąć na zwykłym, płaskim obrazku.
Ze zdrową głową zapraszam Cię na kolejny wpis. Do przeczytania!
Przydatne linki:
Bumpmapping w Wikipedii.
The Fast & The Canvas, czyli szybki dostęp do pikseli na Canvas.
Bitmapa źródłowa z Pixabay.